Laplace Mechanism Basics

The Laplace Mechanism adds noise drawn from a Laplace distribution to realize differential privacy.

This mechanism works well for computing means and histograms, providing accurate results at minimal privacy budgets.

This notebook walks through the basic eeprivacy functions for working with the Laplace Mechanism.

# Preamble: imports and figure settings

from eeprivacy.mechanisms import LaplaceMechanism
from eeprivacy.operations import (
  PrivateClampedMean,
  PrivateHistogram,
)

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import matplotlib as mpl
from scipy import stats

np.random.seed(1234) # Fix seed for deterministic documentation

mpl.style.use("seaborn-white")

MD = 28
LG = 36
plt.rcParams.update({
    "figure.figsize": [25, 10],
    "legend.fontsize": MD,
    "axes.labelsize": LG,
    "axes.titlesize": LG,
    "xtick.labelsize": LG,
    "ytick.labelsize": LG,
})

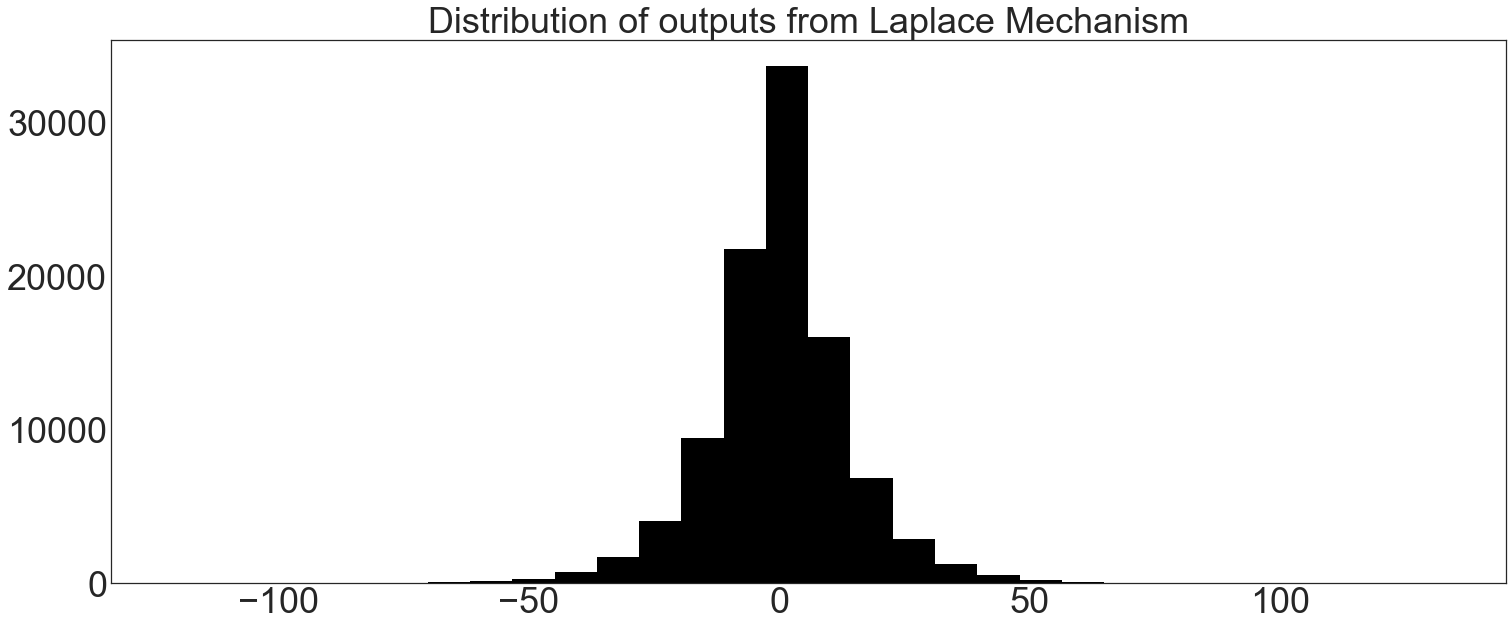
Distribution of Laplace Mechanism Outputs

For a given ε, noise is drawn from the Laplace distribution at b=sensitivity/ε. The eeprivacy class LaplaceMechanism draws this noise and adds it to a private value:

trials = []
for t in range(1000):
  trials.append(LaplaceMechanism.execute(
    value=0,
    epsilon=0.1,
    sensitivity=199/3000
  ))

plt.hist(trials, bins=30, color="k")
plt.title("Distribution of outputs from Laplace Mechanism")
plt.show()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
<ipython-input-1-4ba7af56c713> in <module>
      1 trials = []
      2 for t in range(1000):
----> 3   trials.append(LaplaceMechanism.execute(
      4     value=0,
      5     epsilon=0.1,

NameError: name 'LaplaceMechanism' is not defined

Laplace Mechanism Confidence Interval

With the eeprivacy confidence interval functions, analysts can determine how far away the true value of a statistics is from the differentially private result.

To determine the confidence interval for a given choice of privacy parameters, employ eeprivacy.laplace_mechanism_confidence_interval.

To determine the privacy parameters for a desired confidence interval, employ eeprivacy.laplace_mechanism_epsilon_for_confidence_interval.

The confidence intervals reported below are two-sided. For example, for a 95% confidence interval of +/-10, 2.5% of results will be smaller than -10 and 2.5% of results will be larger than +10.

trials = []
for t in range(100000):
  trials.append(LaplaceMechanism.execute(
    value=0,
    epsilon=0.1,
    sensitivity=1
  ))

plt.hist(trials, bins=30, color="k")
plt.title("Distribution of outputs from Laplace Mechanism")
plt.show()

ci = np.quantile(trials, 0.975)
print(f"95% Confidence Interval (Stochastic): {ci}")

ci = LaplaceMechanism.confidence_interval(
  epsilon=0.1,
  sensitivity=1,
  confidence=0.95
)
print(f"95% Confidence Interval (Exact): {ci}")

# Now in reverse:
epsilon = LaplaceMechanism.epsilon_for_confidence_interval(
  target_ci=29.957,
  sensitivity=1,
  confidence=0.95
)
print(f"ε for confidence interval: {epsilon}")

95% Confidence Interval (Stochastic): 30.05118474953303
95% Confidence Interval (Exact): 29.9573227355399
ε for confidence interval: 0.100001077329305

Examples of Laplace Mechanism Helpers using eeprivacy

The Laplace Mechanism is well-suited for computing means, and eeprivacy provides a helper private_mean_with_laplace for this use case.

The private mean function implemented by eeprivacy employs the “clamped mean” approach to bound sensitivity. Analysts provide a fixed lower_bound and upper_bound before computing the mean. For datasets with unknown ranges, an approach like the one described in [Computing Bounds for Clamped Means] can be used.

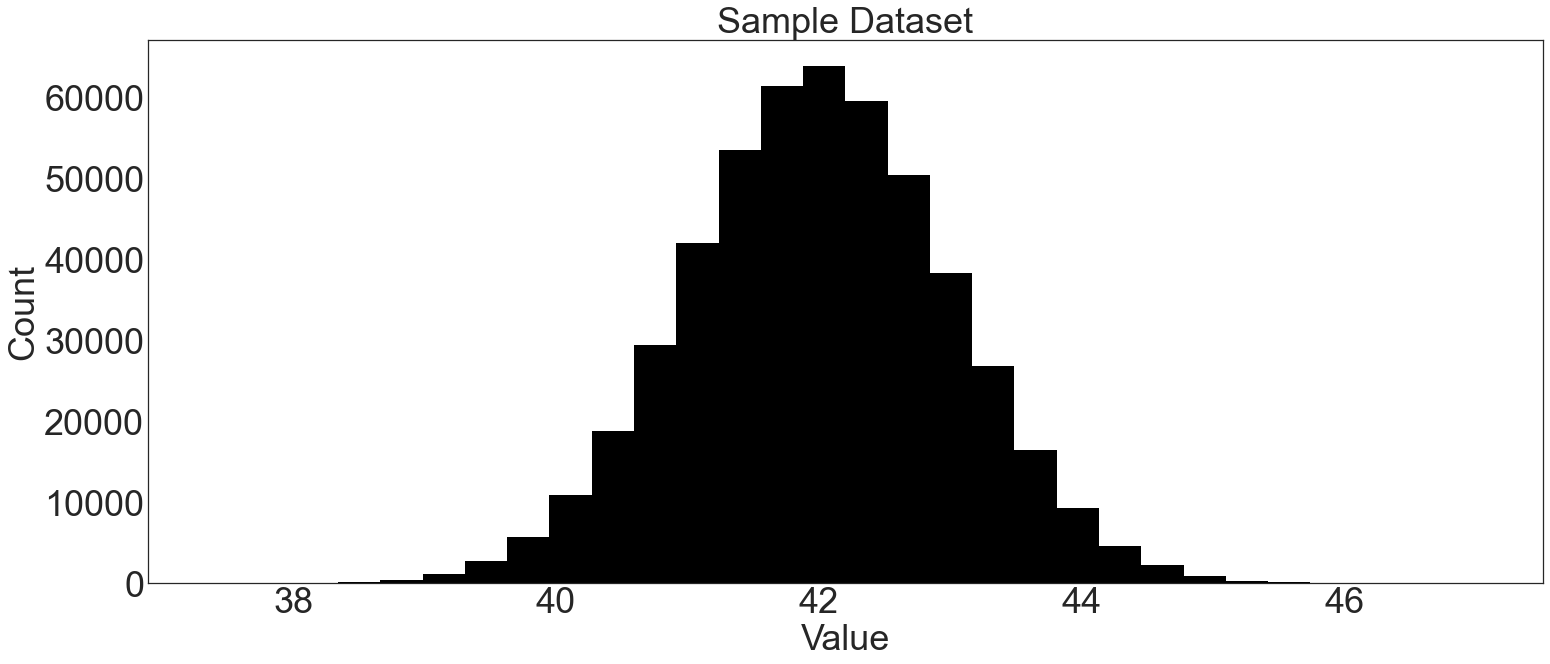
N = 500000
dataset = np.random.normal(loc=42, size=N)

plt.hist(dataset, bins=30, color="k")
plt.title("Sample Dataset")
plt.xlabel("Value")
plt.ylabel("Count")
plt.show()

trials = []

private_mean_op = PrivateClampedMean(
  lower_bound = 0,
  upper_bound = 50
)

for i in range(1000):
  private_mean = private_mean_op.execute(
    values=dataset,
    epsilon=0.1,
  )
  trials.append(private_mean)

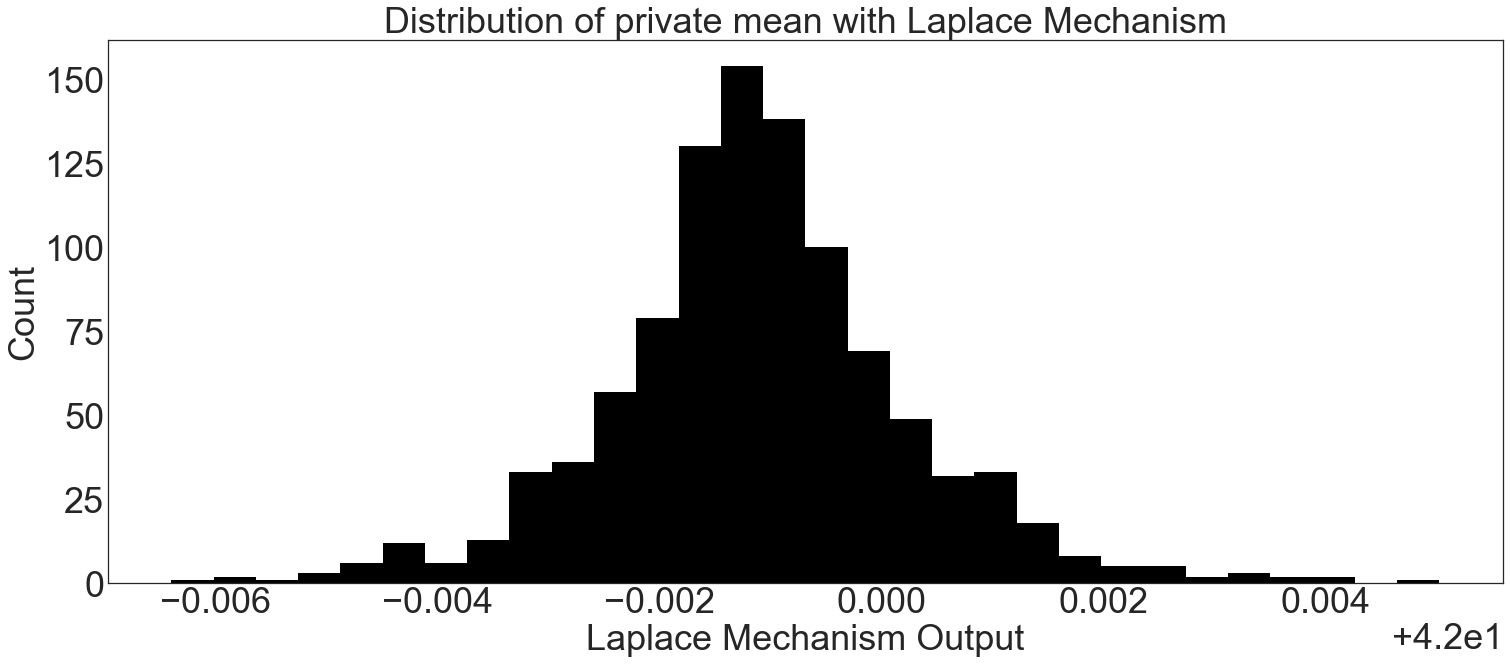
plt.hist(trials, bins=30, color="k")
plt.title("Distribution of private mean with Laplace Mechanism")
plt.xlabel("Laplace Mechanism Output")
plt.ylabel("Count")
plt.show()

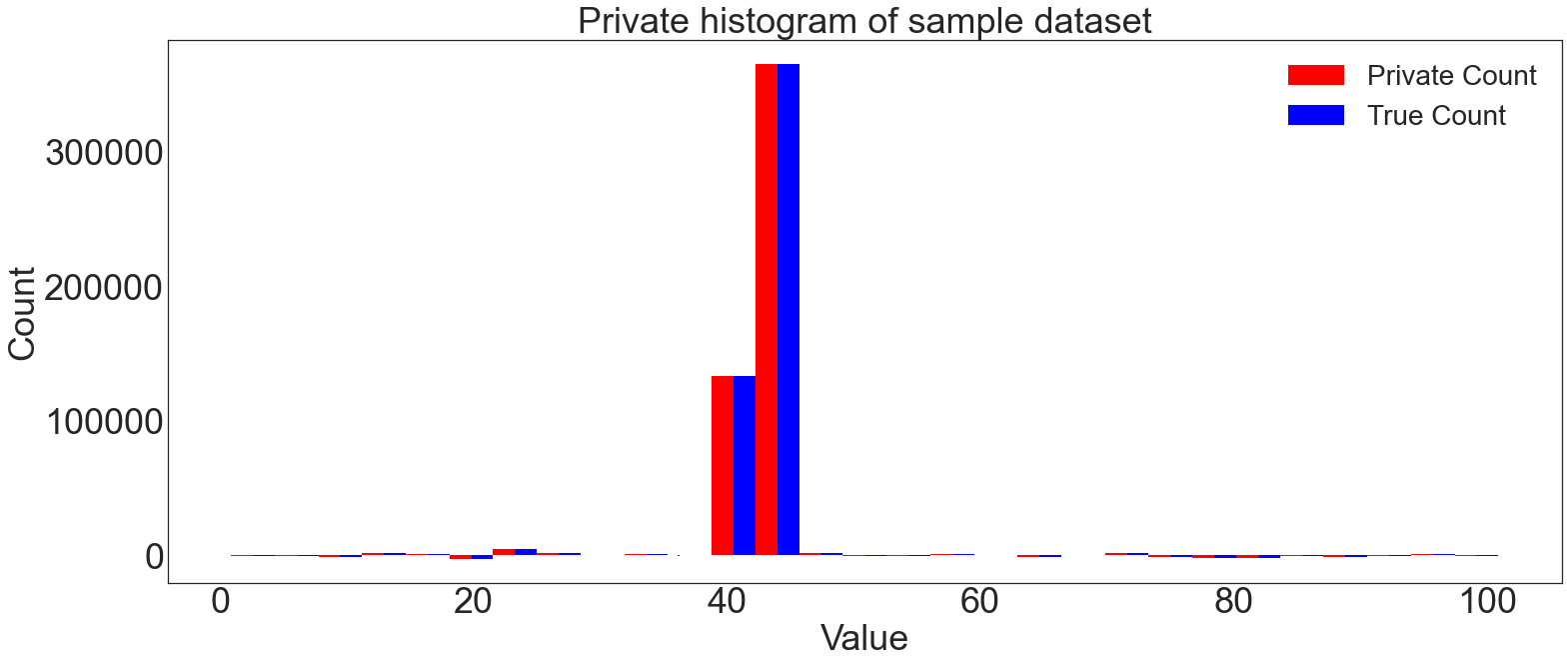
Computing Private Histograms

The Laplace Mechanism is also well-suited for private histograms.

bins = np.linspace(start=0, stop=100, num=30)

private_histogram_op = PrivateHistogram(
  bins = bins,
)

private_histogram = private_histogram_op.execute(
  values=dataset,
  epsilon=0.001
)

true_histogram = np.histogram(dataset, bins=bins)

bin_centers = (bins[0:-1] + bins[1:]) / 2
bin_width = bins[1] - bins[0]

fig, ax = plt.subplots()
ax.bar(
  bin_centers,
  private_histogram,
  width=bin_width/2,
  yerr=ci,
  color="r",
  label="Private Count"
)
ax.bar(
  bin_centers+bin_width/2,
  private_histogram,
  width=bin_width/2,
  color="b",
  label="True Count"
)

plt.title("Private histogram of sample dataset")
plt.xlabel("Value")
plt.ylabel("Count")
plt.legend()
plt.show()